Actual Effort in Cognitive Tasks (pt 2)
Recap
You can read part 1 of my exploration of using Item Response Theory (IRT) for operationalisation of actual effort in cognitive tasks here.
But here’s a very quick TLDR recap of the thinking from its conclusion:
“Key assumptions underlying IRT models and their parameters, ability and difficulty, map conceptually well onto the assumed primitives, capacity and demands, in my definition of effort. Given this, IRT models seem like a useful approach to operationalisation of actual effort in cognitive tasks. In fact, using the example of a test involving lifting weights where we actually know a persons underlying ability/capacity and the difficulty/demands of each item in the test, the estimates of effort that result from an IRT model are pretty reasonable estimates of the actual effort we could calculate from direct measurements.”
In the post, I used the analogy of testing the ability of ‘strength’ through lifting different loads and fit a 1-parameter logistic (1PL, or Rasch model) to some simulated data representing people with varying strength levels lifting different loads successfully or not depending on this. This toy example demonstrated quite nicely (if I do say so myself) that in principle we can use IRT models to estimate the actual effort required for a given person performing a given task/item. As a result, I think it could be a promising approach to exploring effort psychophysics in cognitive tasks i.e., the relationship between actual effort, and perception of effort.
But how does it work out when we introduce it to some real data? I got hold of a dataset where I was able to fit IRT models to the cognitive tasks performed, and where they had also captured some operationalisation of perception of effort.
Measurement scale issues
Before I get to the actual dataset, we first need to talk about the issues with IRT models for my ideas about estimating effort as:
\[\theta_{j}=C_{A(j)}\] \[\beta_{i}=D_{A(i)}\]
\[\beta_{i} \leq \theta_{j} \Rightarrow E_{A(ji,IRT)} = \frac{ \beta_{i}} {\theta_{j}} \times 100%\]
\[\beta_{i} > \theta_{j} \Rightarrow E_{A(ji,IRT)} = 100%\]
Where, for each person we test \(j(j=1,...,J)\), and each item in a test they complete \(i(i=1,...,I)\), \(\theta_{j}\) is the IRT estimated person latent ability, \(C_{A(j)}\) is the actual capacity, \(\beta_{i}\) is the IRT estimated item difficulty parameter, \(D_{A(i)}\) is the actual item demands, and \(E_{A(ji,IRT)}\) is the actual effort that it is estimated from the IRT model.
A problem is that common IRT models are typically estimated on the \(logit\) scale which ranges \(-\infty,\infty\). This poses some problems for us when it comes to calculating \(E_{A(ji,IRT)}\) from the ratio of \(\beta_{i}\) to \(\theta_{j}\) as \(logit\) scale does not have ratio properties. Now, I did mention that there are various ways of transforming the \(logit\) scale that both preserves the underlying probabilities for a given \(\theta\) completing a given item with difficulty \(\beta\). For example, the 1PL model can undergo linear transformation without altering the underlying mathematical model and we can have \(\theta_{transf}\) and \(\beta_{transf}\). This gave me the idea for the weight lifting toy example. Given I had the \(C_{A(j)}\) because I simulated it, and had also chosen the \(D_{A(i)}\) which these simulated people would try to meet, and all in its raw units (kg), once I had fit the 1PL model I could fit simple linear models to transform \(\theta_{j}\) and \(\beta_{i}\) back to the raw kg units \(\theta_{j(transf)}\) and \(\beta_{i(transf)}\).
However, I hit a bit of a snag thinking through this with typical cognitive tasks. It’s not as simple as with my toy example to put \(\theta_{j}\) and \(\beta_{i}\) onto ratio scales in a meaningful way… For example, It seems ontologically odd to me to have ability on the logit scale. I mean, does anyone really conceptualise \(\theta_{j}\) in some task as really ranging from \(-\infty,\infty\)? Do we not think there’s at least some floor (i.e., you can’t do any difficulty item)? Also, transformation back to sum scores, or even proportions accurate (akin to the test characteristics curve) seems odd for \(\beta_{i}\).
Odd?
Oh, then it suddenly hit me… \(\theta_{j}\) and \(\beta_{i}\) could be placed back onto ratio scales in a meaningful way: the odds scale.
This approach is somewhat limited to the application of 1PL/Rasch type IRT models1 but it’s something to start with.
Under the odds formulation of the 1PL/Rasch model we estimate actual effort in cognitive tasks as:
\[exp(\theta_{j})=C_{A(j)}\] \[exp(\beta_{i})=D_{A(i)}\]
\[exp(\beta_{i}) \leq exp(\theta_{j}) \Rightarrow E_{A(ji,IRT)} = \frac{ exp(\beta_{i})} {exp(\theta_{j})} \times 100%\]
\[exp(\beta_{i}) > exp(\theta_{j}) \Rightarrow E_{A(ji,IRT)} = 100%\]
It’s not clear to me how good this should be as an operationalisation given it’s hard to validate this derivation of \(E_{A(ji)}\) against its derivation from some direct measurement of the underlying constructs \(C_{A(j)}\) and \(D_{A(i)}\) in their raw units. But, working with the assumption as I do that…
“…the perception of effort appears at best a coarsegrained representation of actual effort which is probably a result of the introduction of ‘noise’ into the signal from both the sensory systems, and the perceptual system. As such, although the directional patterns of perception of effort often follow those we would expect based upon actual effort, they are ‘fuzzy’ and inaccurate representations of reality.”2
…we’d expect at the very least to see positive directional relationships between our IRT operationalisation of actual (objective) effort (i.e., \(E_{A(ji,IRT)}\)) and operationalisations of perception of (subjective) effort, or subjective effort. I’d consider this directional relationship to at least be some indication that we’re on the right path in terms of operationalisation.
So let’s take a look at a real example dataset and see how things turn out.
N-Back tasks, NASA-TLX, and Effort Discounting
Andrew Westbrook was kind enough to share with me all the data from his 2013 PloS One study with Daria Kester and Todd Braver:
In this study both young and old adults performed the N-Back task3 over varying difficulty levels (1-6-Back). They also captured two different operationalisations related to the subjective nature of effort. Firstly, they captured the NASA Task Load Index (NASA-TLX)4 which here I assume is an operationalisation of the perception of effort i.e., the phenomenological experience. Secondly, they also determined the subjective value (\(SV\)) of effort using a cognitive effort discounting paradigm5 which I’m not sure is wholly reflective of the perception of effort per se6 but is interesting to explore nonetheless. Here I reverse it to be the subjective cost of effort (i.e., \(1-SV\)) So in all we have a cognitive task (N-Back) which we can apply an IRT model to in order to operationalise the actual (objective) effort, and a couple of different operationalisation of the perception of (subjective) effort.
So firstly let’s fit the 1PL model to the N-Back data treating each level (1-6) as an item. Here’s the Item Characteristic Curves across the items:
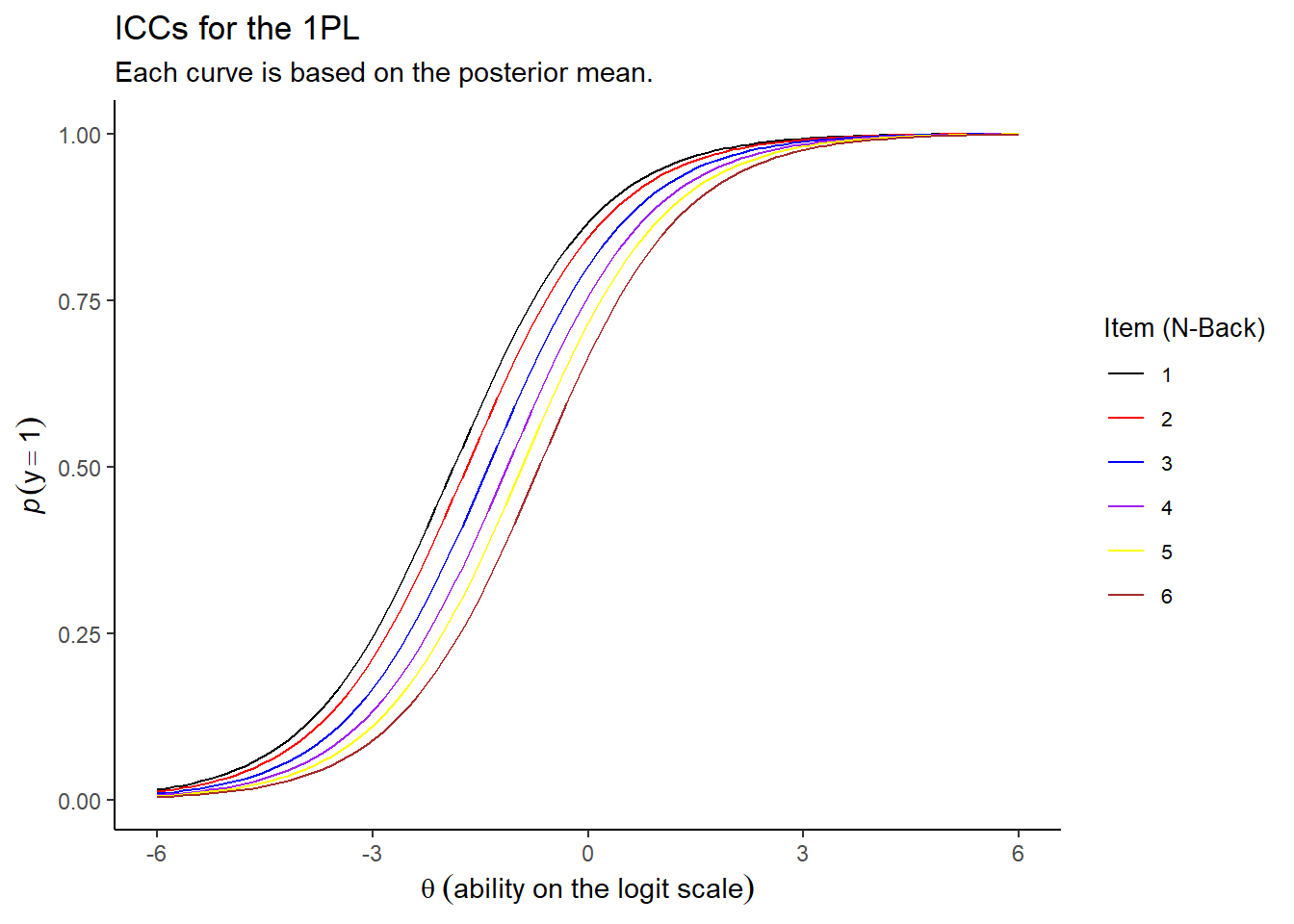
Nice. The 1PL model shows what we would expect from increasing N-Back: that the difficulty of each item increases with the N trials ago that someone is trying to remember.
From this we can pull out the random effects for person and item, \(\theta_{j}\) and \(\beta_{i}\), and then we can exponentiate them to put them back on the odds scale to calculate \(E_{A(ji,IRT)}\). Then we rejoin it with the effort scale from the NASA-TLX, and the subjective cost of effort determined from the effort discounting paradigm, and can begin to model the relationship between \(E_{A(ji,IRT)}\) and both these operationalisations of perception of (subjective) effort.
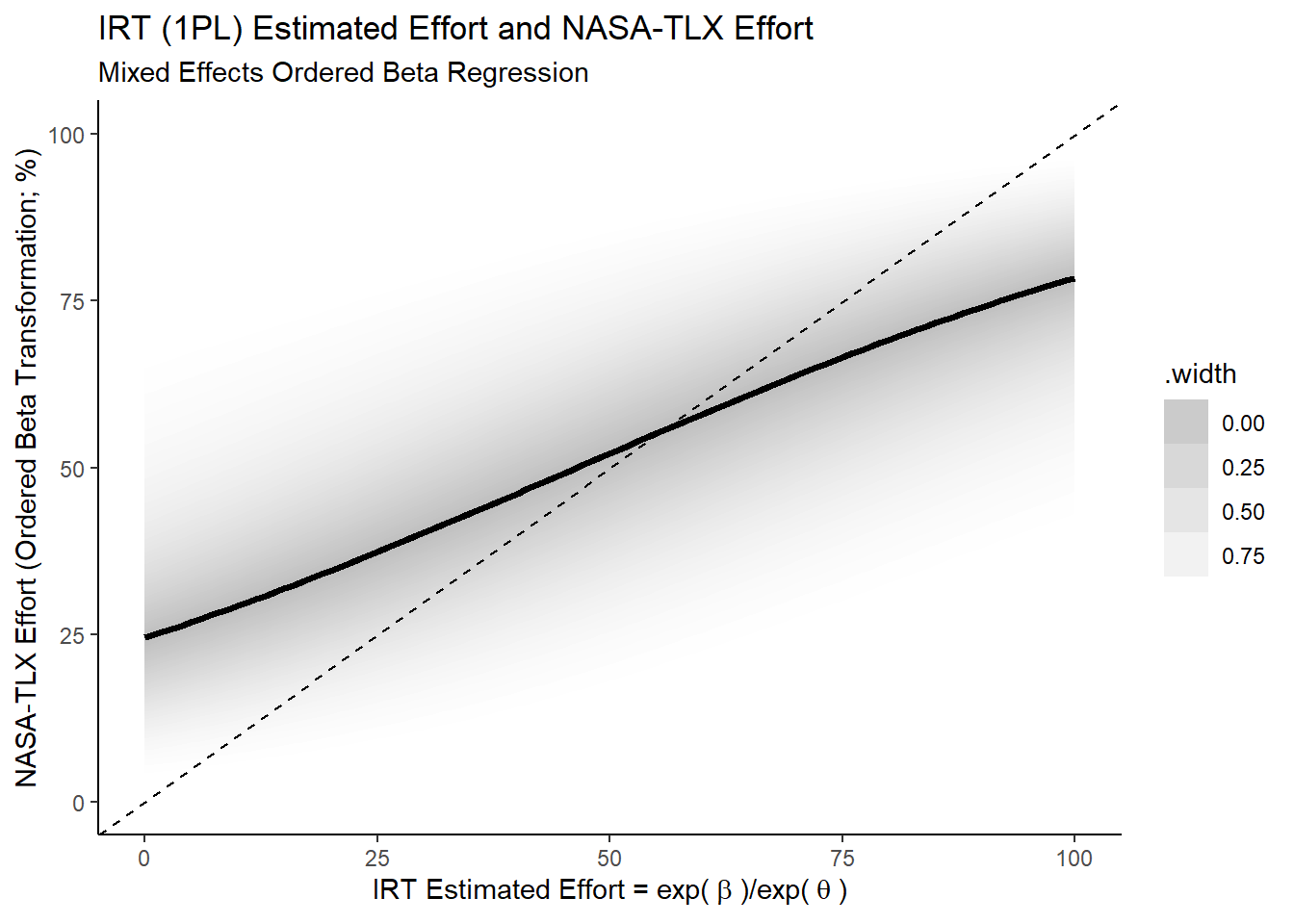
First we will look at the NASA-TLX data. Now, the NASA-TLX is an ordinal scale and so we might consider using cummulative ordinal regression on the probit scale. But this model assumes that the data arises from unbounded normal distributions where our underlying latent variable of perception of effort is conceptually bounded. So we should use a model to reflect that such as ordered beta regression7. Similarly to the previous post we fit a mixed effects model with random intercepts and slopes to explore how well \(E_{A(ji,IRT)}\) is related to the Effort scale of the NASA-TLX.
And we then do the same for the subjective cost of effort.
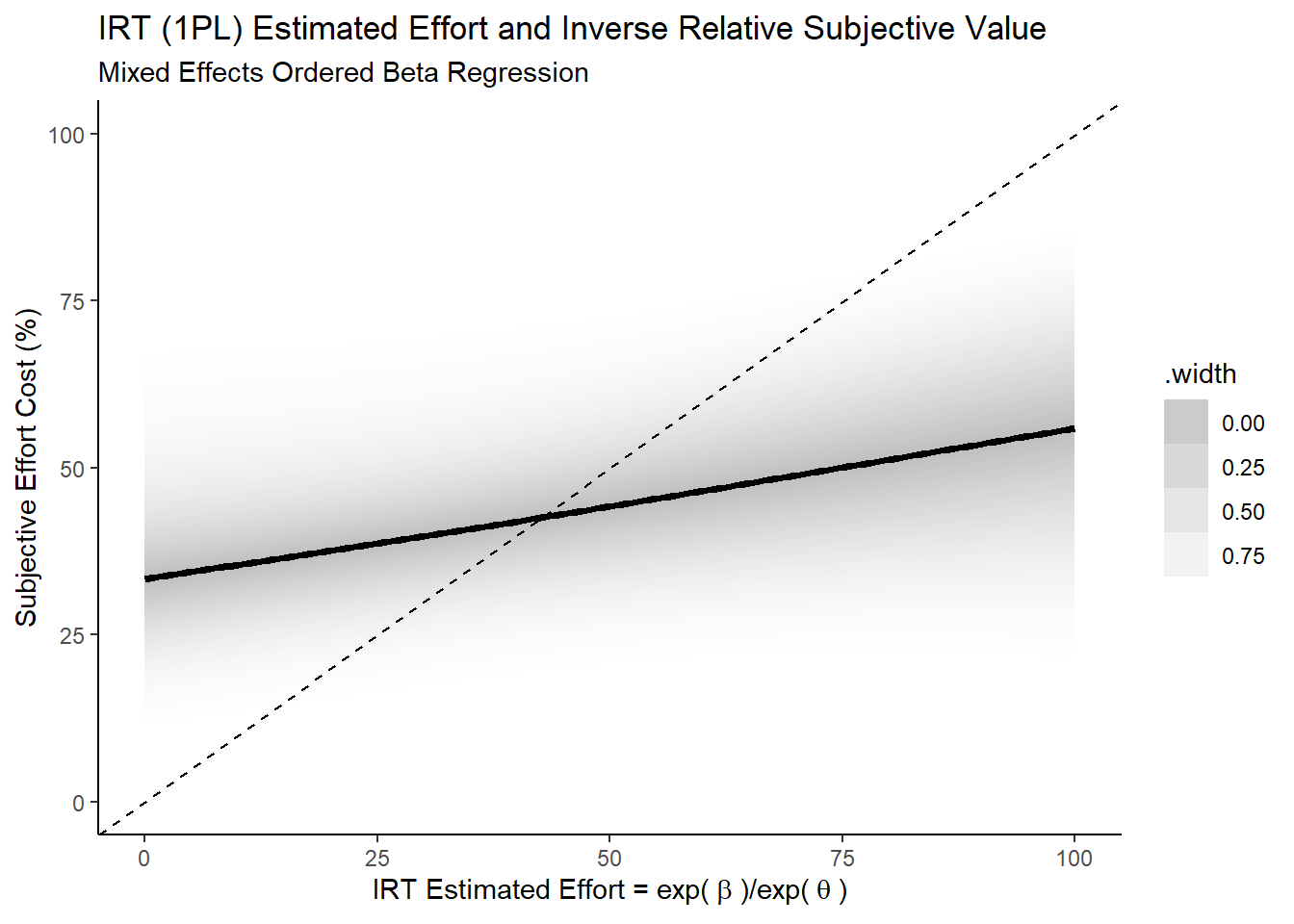
Ok, so both show the sort of positive directional relationship I’d expect to see if this operationalisation of actual effort were at least somewhat valid: for tasks that require higher actual effort, people seem to have the subjective experience that they do indeed require more effort8.
It’s also interesting to see that this relationship is closer to the identity for the NASA-TLX Effort scale as compared to the subjective cost. This seems unsurprising given that the NASA-TLX Effort scale asks more directly about the magnitude of the phenemenological experience of effort while the subjective cost, despite likely being informed by the magnitude of the perception of effort, isn’t necessarily directly about that phenomenological experience itself.
Summary and Conclusion
As discussed, IRT models have assumptions and parameters, ability and difficulty, that map conceptually well onto the assumed primitives, capacity and demands, in my definition of effort and as such seem like a useful approach to exploring operationalisation of actual effort in cognitive tasks. But, it’s not always obvious how to convert \(\theta_{j}\) and \(\beta_{i}\) from interval scale logits onto ratio scales in a meaningful way. However, the odds scale formulation of the 1PL/Rasch model is one approach that may work. Here I used a dataset from a previous study and explored relationships between our IRT based operationalisation of actual effort and operationalisations of the perception of effort. As might be expected there were positive directional relationships between these operationalisations, and the relationship was stronger for operationalisations of the pheneomenological experience of effort that had stronger construct, or at least face, validity.
This is encouraging to see and makes me think it is worthwhile looking to explore this in other datasets, and also to begin to systematically collect data for cognitive tasks amenable to these models9.
See this nice thesis by Rebecca Freund Rasch and Rationality: Scale typologies as applied to Item Response Theory↩︎
What is (perception of) effort? Objective and subjective effort during attempted task performance↩︎
Free demo of the 2-back task as an example here for those that don’t know what this involves… at the higher levels it’s pretty tough.↩︎
The NASA-TLX is a six item state questionnaire, one of which asks about the effort required i.e., “How hard did you have to work to accomplish your level of performance?”. It’s not ideal in my opinion given my conceptual definition of perception of effort, but it’ll do for current purposes.↩︎
Westbrook et al. describe it as follows: “The key feature of this paradigm is that participants choose whether to perform a low-effort task for a small monetary reward or a high-effort task for a larger reward (Figure 1). Multiple choices are made, and the amount offered for the low-effort task is titrated until subjective equivalence is reached (the offers are equally preferred). The additional amount required to make the high- and low-effort task equivalent quantifies the cost of cognitive effort, or the degree to which increased cognitive effort diminishes the value of task engagement. The objective load of the high-effort task can also be varied parametrically. As such, the procedure is formally analogous to the estimation of discounting across a range of delays in delay discounting. Unlike discounting procedures involving hypothetical costs or rewards, participants make choices about tasks that they are actually paid for re-doing, promoting test validity.”↩︎
It is often assumed that effort is inherently aversive and so the valuation of effort says something about the subjective experience of it. But as Inzlicht et al. have suggested effort can be both costly and valued. In fact, some people often seek out effortful experiences. For example, I like to engage in resistance training, and when I do so I deliberately aim to do so with maximum effort (i.e., to task failure). In such a situation the subjective valuation of the effort experienced would not necessarily follow the direction which would be assumed if it were inherently aversive.↩︎
As with the previous post I use the {ordbetareg} package that overlays {brms}, from Robert Kubinec see here and which does the job of normalising the variable to the [0,1] interval to fit the ordered beta regression model.↩︎
Although, it is interesting that people seem to over- and under-estimate at lower and higher actual efforts respectively. The topic of this with respect to proportions/percentages came up in a recent twitter thread from Dan Goldstein and Toph Tucker also put this simulation together to explore the influence of informed and random guesses, as well as the variance in guesses. It did make me wonder though whether assuming that proportion estimates come from a normal, or even truncated normal distribution might be influencing this pattern as opposed to assuming they come from say a beta distribution. So I had a little play with this (see thread here). This is something I might come back to explore a bit more at some stage.↩︎
I have had the idea for a while to use Raven’s Progressive Matrices for this given the number of items and their progressive nature (I always thought of it as a sort of “cognitive one-rep max”). For each item participants complete we would capture a self-report of the perception of effort required to complete that item on a 0-100% scale. Then we could look at fitting these kinds of models to explore the relationships.↩︎
James Steele
Associate Professor of Sport and Exercise Science
James is Associate Professor of Sport and Exercise Science at Solent University, and Director of Steele Research Ltd. Effort, and its perception, has interested him for the past decade starting with the field of sport and exercise before broadening towards effort across all task domains. Horme Lab represents James' efforts at better conceptualising, theorising, and investigating this area.